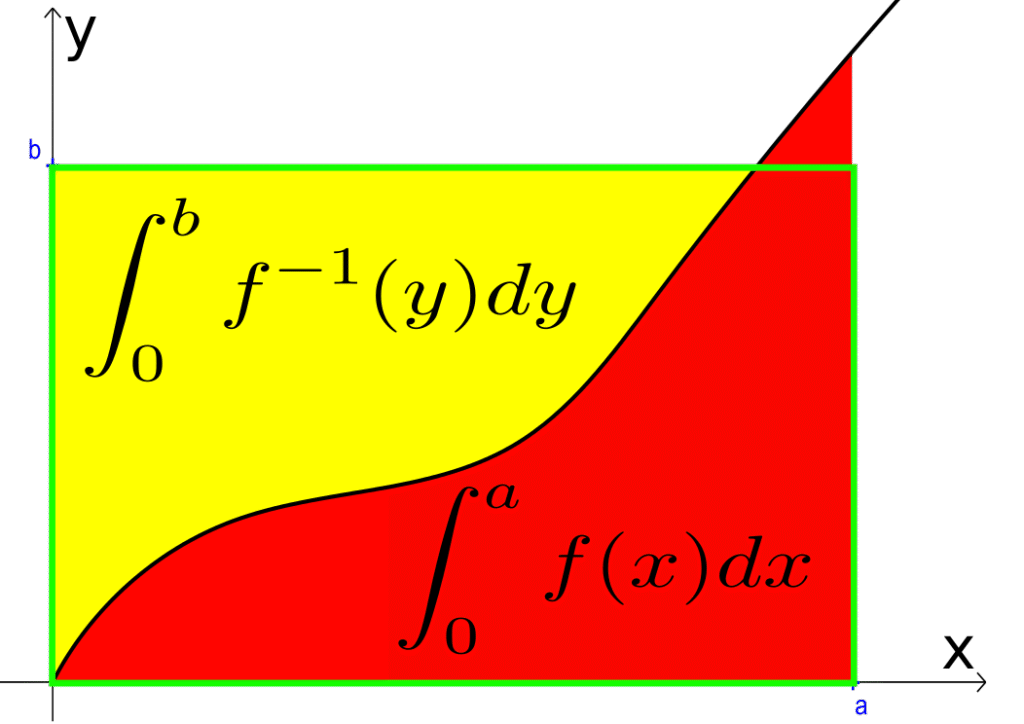
Calculus inequalities using inverse function integrals
I recently encountered this beautiful problem in Crux Magazine (OC726) that initially seemed quite intimidating, but turned out to have a surprisingly elegant solution once you find the right perspective. Usually in school we are asked to integrate explicit functions. Is it possible to integrate implicit functions? For instance, suppose we know that g(x) is […]