Calculus inequalities using inverse function integrals

I recently encountered this beautiful problem in Crux Magazine (OC726) that initially seemed quite intimidating, but turned out to have a surprisingly elegant solution once you find the right perspective.

Usually in school we are asked to integrate explicit functions. Is it possible to integrate implicit functions? For instance, suppose we know that g(x) is the inverse function of an explicit integrable function f(x), can we compute a definite integral $\int g(x) dx$? Yes! we can. I will state the theorem along the way.

The Problem

OC725: Let $f : \mathbb{R} \to \mathbb{R}$ be a continuous function such that $f(x) + \sin(f(x)) \geq x$ for all $x \in \mathbb{R}$. Prove that:

$$\int_0^\pi f(x) \, dx \geq \frac{\pi^2}{2} – 2$$

Aha! Moment

At first glance, this constraint $f(x) + \sin(f(x)) \geq x$ looks rather unwieldy. My initial instinct was to try various substitutions or perhaps some clever inequalities, but nothing seemed to lead anywhere productive. The breakthrough came when I realized that the expression $f(x) + \sin(f(x))$ is simply a composition of the function $g(t) = t + \sin(t)$ and $f(x)$. So it makes sense to first study $g(t)$. Further note that the given condition is simply $g(f(x)) \geq x$. Now if only g was an increasing function, we will have $f(x) \geq g^{-1}(x)$. Here’s where the magic happens. We can use the beautiful relationship between integrals of inverse functions. For any strictly increasing function $g$ on an interval $[a,b]$, we have:

$$\int_a^b g(t) \, dt + \int_{g(a)}^{g(b)} g^{-1}(x) \, dx = b g(b) – a g(a).$$

Here is a picture proof where $b=f(b)=0$.

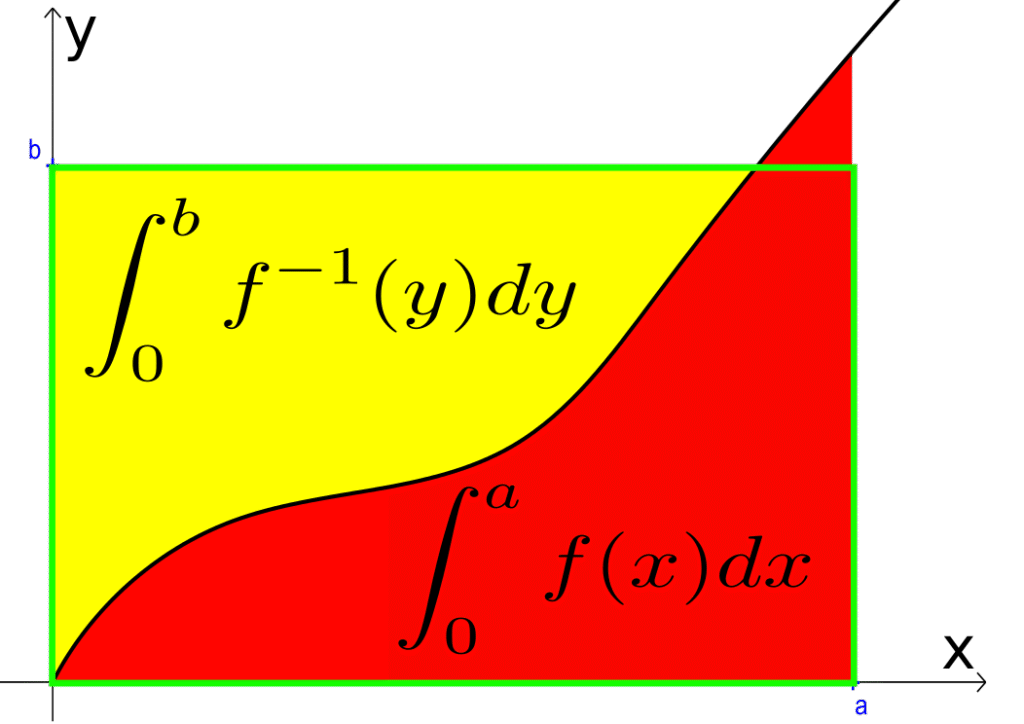
After all these steps, will the math overlords bless us with the correct right hand side bound? The answer is YES!!

CLICK HERE to see the PROOF

Let $g(t) = t +\sin t$. Since $g'(t) = 1 + \cos(t) \geq 0$, the function $g$ is monotonically increasing, which means it has an inverse on its range. The constraint $f(x) + \sin(f(x)) \geq x$ becomes $g(f(x)) \geq x$, and by the monotonicity of $g$, this gives us $f(x) \geq g^{-1}(x)$. So now we need to find $\int_0^\pi g^{-1}(x) \, dx$.

In our case, $g(0) = 0$ and $g(\pi) = \pi + \sin(\pi) = \pi$, so this becomes:
$$\int_0^\pi g(t) \, dt + \int_0^\pi g^{-1}(x) \, dx = \pi^2$$

The direct integral is straightforward to compute:
$$\int_0^\pi (t + \sin t) \, dt = \frac{\pi^2}{2} + [-\cos t]_0^\pi = \frac{\pi^2}{2} + 2$$

Therefore: $\int_0^\pi g^{-1}(x) \, dx = \pi^2 – \left(\frac{\pi^2}{2} + 2\right) = \frac{\pi^2}{2} – 2$

Since $f(x) \geq g^{-1}(x)$, we immediately get our desired result: $\int_0^\pi f(x) \, dx \geq \frac{\pi^2}{2} – 2$.

Why This Approach is Beautiful

What I love about this solution is how it sidesteps all the technical difficulties that initially seemed unavoidable. Instead of wrestling with transcendental equations or hunting for clever bounds, the inverse function integral theorem gives us exactly what we need. It’s a perfect example of how knowing the right theorem can transform a seemingly difficult problem into something quite manageable. Also as a student, you should appreciate the power of inverse function theorem.

The geometric intuition is also quite nice: the theorem essentially says that the area under a curve plus the area under its reflection across the line $y = x$ equals the area of a rectangle. This geometric relationship, when applied to our specific function $g(t) = t + \sin(t)$, yields the precise bound we need.

---

JEE Exercise: Check out Q3 in JEE 2022 paper here. For your benefit, here is the question:

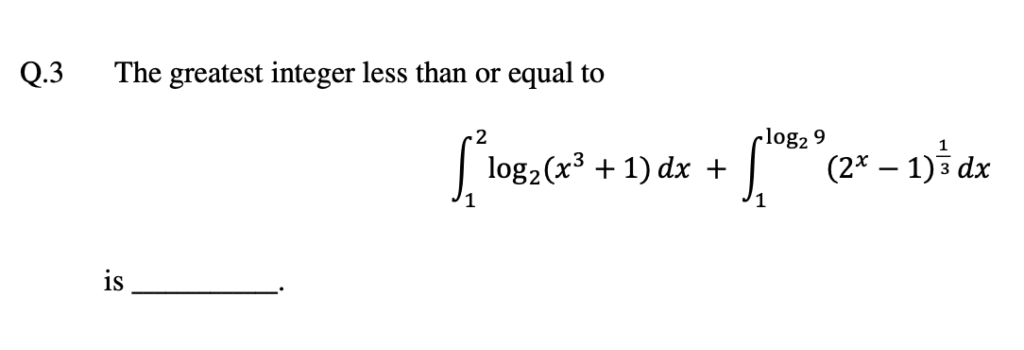
Have you encountered other problems where finding the right perspective completely changed the difficulty? I’d love to hear about similar experiences in the comments!

Tags: #RealAnalysis #Integration #InverseFunctions #MathematicalProofs #ProblemSolving #JEEProblems