Note: This was posted immediately after RMO 2024 on 3/11/2024.
I solved the RMO problems today after the exam. I am documenting the solutions and my feelings of difficulty (out of 5) for each problem. I hope you enjoy the solutions. Let me know if you liked it, and share the solutions with interested people.

RMO difficulty feeling: 1.
Straightforward problem. The invariant of part a is standard. The second part is not too convoluted and is something most people will try. It’s a good beginner problem that sets the mood and eases the participant.
Proof:
(a) Suppose \( n \) is odd and \( a_1, a_2, \ldots, a_n \) is a nice rearrangement. Since \( a_1, a_2, \ldots, a_n \) is a permutation of \( 1, 2, 3, \ldots, n \), it is immediate that
$$
a_1 + a_2 + a_3 + \ldots + a_n = 1 + 2 + 3 + \ldots + n = \frac{n(n+1)}{2}.
$$
Since \( n \) is odd, we note that \( \frac{n(n+1)}{2} \) is a multiple of \( n \) since \( n+1 \) is even. This contradicts the niceness of the rearrangement since the sum \( a_1 + a_2 + a_3 + \ldots + a_n \) is a multiple of \( n \).
(b) If \( n \) is even, we claim the rearrangement \( 2,1,4,3,6,5,8,7,\ldots,n,n-1 \) is always nice.
The proof is by induction on \( n \). For \( n=2 \), clearly \( 2,1 \) is nice since 2 does not divide 3.
Suppose we have proved the claim for some even \( n \), then we show the claim holds for \( n+2 \).
For \( n+2 \), we already know \( a_1 + a_2 + a_3 + \ldots + a_k \) is not a multiple of \( k \) for \( k \leq n \) by induction.
Next we note that:
$$
a_1 + \ldots + a_{n+1} = \frac{n(n+1)}{2} + (n+1) + 1
$$
which leaves a remainder of 1 when divided by \( n+1 \), since the first two terms are multiples of \( n+1 \).
And finally,
$$
a_1 + a_2 + a_3 + \ldots + a_{n+2} = \frac{(n+2)(n+3)}{2}.
$$
The number \( \frac{(n+2)(n+3)}{2} \) is not divisible by \( n+2 \), since the quotient \( \frac{(n+3)}{2} \) is a fraction (because \( n+3 \) is odd).
Thus \( a_1 + a_2 + a_3 + \ldots + a_{n+2} \) is not a multiple of \( n+2 \).
Hence, the claim is proved for \( n+2 \). So the proof of the statement
“the rearrangement \( 2,1,4,3,6,5,8,7,\ldots,n,n-1 \) is always nice” is complete.
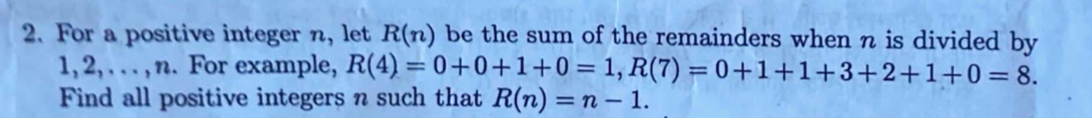
RMO difficulty feeling: 2.
Straightforward to guess the answer by trial and error. But proving it requires you to note that \( R(n) > n \) eventually. Now \( R(n) \) grows as \( n^2 \), so there will be many ways to do this proof. The proof writing is the main focus of this question since the idea is pretty simple. It’s rated 2 because the algebra can get messy for a beginner.
Proof: The key idea is to note that by division algorithm if \( a,b \) are natural numbers, then
$$
a = \left\lfloor \frac{a}{b} \right\rfloor b + r
$$
where \( r \) is the remainder when \( a \) is divided by \( b \).
So we have a formula for \( R(n) \):
$$
R(n) = \sum_{k=1}^n \left(n – \left\lfloor\frac{n}{k}\right\rfloor k\right)
$$
We note that for \( n \geq k > n/2 \), we have \( 1 \leq \frac{n}{k} < 2 \). Thus \( \lfloor n/k\rfloor = 1 \) for this range. The terms in this range are summable and we thus obtain a bound for all \( n \):
$$
R(n) \geq \sum_{k > \lceil n/2\rceil}^n (n-k) = 1+ 2 +\ldots + \left(\lceil n/2 \rceil -1\right) \geq \dfrac{n/2(n/2-1)}{2} = \dfrac{n(n-2)}{8}.
$$
In the problem, we want to solve for \( R(n) = n-1 \). Suppose \( m \) solves the equation, then
$$
m-1 = R(m) \geq \dfrac{m(m-2)}{8}.
$$
Thus we solve the quadratic inequality:
$$
8m – 8 \geq m^2 – 2m \Rightarrow m^2 – 10m + 8 \leq 0 \Rightarrow m \leq 9.
$$
So we have to check the first 9 numbers only:
Thus \( 1,5 \) are the only solutions.
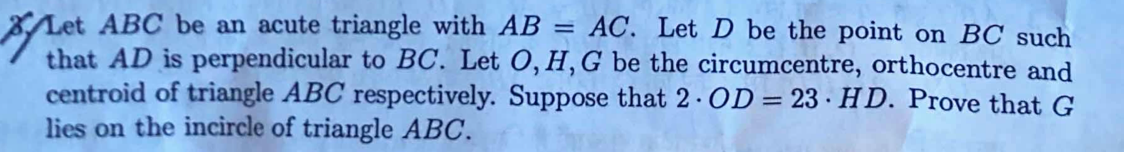
RMO difficulty feeling: 3.
I wonder if there is a synthetic solution. All the lengths in the problem make it clear that most solutions will mostly be length bash based. Since there is a busy right angled point (D), it is suitable for a coordinate bash.
Sophisticated coordinates computation is not a part of school syllabus and further one should either know various facts or compute heavily to get the relation between coordinates and figure out \( a^2=24 \).
Proof: The proof is a straightforward coordinate computation. We have labelled the circumcentre as S instead of O. Look at the diagram below where S, G, I, H are the circumcentre, centroid, incentre and orthocentre of triangle \( ABC \), respectively.
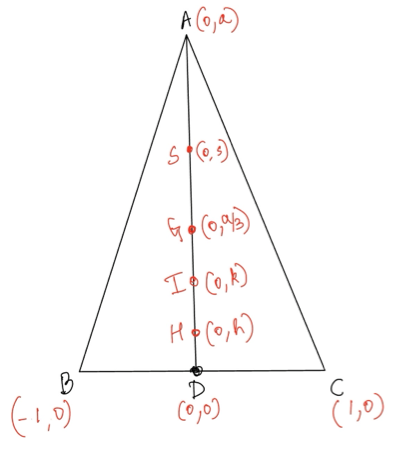
Note that \( G = (0, \frac{a}{3}) \). It is well known that G trisects the segment SH (Euler line), so:
$$
2(0,s)+(0,h) = 3(0,a/3) \Rightarrow 2s + h = a
$$
It is given that \( 2|DS| = 23|HD| \), hence:
$$
2s = 23h \Rightarrow h = \frac{a}{24}, \quad 2s = \frac{23a}{24}
$$
Since \( S \) is the circumcentre, we must have:
$$
(s – a)^2 = s^2 + 1 \Rightarrow a^2 – 2as = 1 \Rightarrow a^2 – \frac{23a^2}{24} = 1 \Rightarrow a^2 = 24
$$
Now compute:
$$
|AB| = |AC| = \sqrt{a^2 + 1} = 5, \quad |BC| = 2
$$
Using the angle bisector lemma, I divides \( AD \) in the ratio \( AB:BD = 5:1 \), so:
$$
\frac{|AI|}{|ID|} = 5 \Rightarrow I = \frac{5(0,0) + 1(0,a)}{6} = \left(0, \frac{a}{6} \right)
$$
Since \( ID \perp BC \), D is the touch point of the incircle with line BC, so \( ID \) is a diameter. G lies on \( ID \), and if \( I \) is midpoint of \( GD \), then \( G \) lies on the incircle.
Check midpoint:
$$
M = \frac{G + D}{2} = \frac{(0, \frac{a}{3}) + (0,0)}{2} = \left(0, \frac{a}{6} \right) = I
$$
So \( G \) lies on the incircle of \( \triangle ABC \).
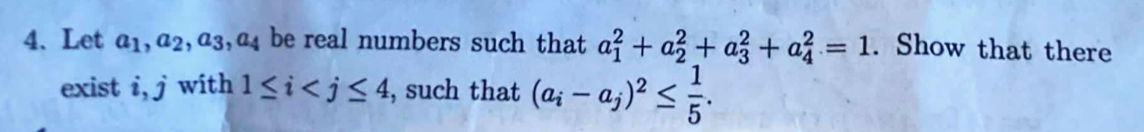
RMO difficulty feeling: 5
This is the hardest problem in the set. I tried various inequalities (AM-GM, Cauchy), but none worked. Brute force algebra finally did. The struggle made this feel like a 5.
Proof: We will prove the inequality by contradiction. In fact we will contradict the constraint
$$
a_1^2 + a_2^2 + a_3^2 + a_4^2 = 1.
$$
Without loss of generality, assume \( a_4 \leq a_3 \leq a_2 \leq a_1 \). Suppose for all \( 1 \leq i < j \leq 4 \),
$$
(a_i – a_j)^2 > \frac{1}{5}.
$$
Thus we have
$$
a_1 – a_2 > \frac{1}{\sqrt{5}}, \quad a_2 – a_3 > \frac{1}{\sqrt{5}}, \quad a_3 – a_4 > \frac{1}{\sqrt{5}}.
$$
Now set
$$
a_1 – a_2 – \frac{1}{\sqrt{5}} = x, \
a_2 – a_3 – \frac{1}{\sqrt{5}} = y, \
a_3 – a_4 – \frac{1}{\sqrt{5}} = z,
$$
and note that \( x, y, z > 0 \). Rearranging and back-substituting the variables we get
$$
a_3 = a_4 + \frac{1}{\sqrt{5}} + z, \
a_2 = a_4 + \frac{2}{\sqrt{5}} + y + z, \
a_1 = a_4 + \frac{3}{\sqrt{5}} + x + y + z.
$$
Now it can be shown that (meaning you should do some work!)
The expression on the right-hand side is greater than one, since \( x, y, z > 0 \), which contradicts the given constraint.

RMO difficulty feeling: 1.5
Pleasant, trigonometry-based cyclic quad problem. Cute enough to include in my geometry lectures.
Proof: Use sine rule.
Let \( R \) be the radius of the circle. Refer to this figure:
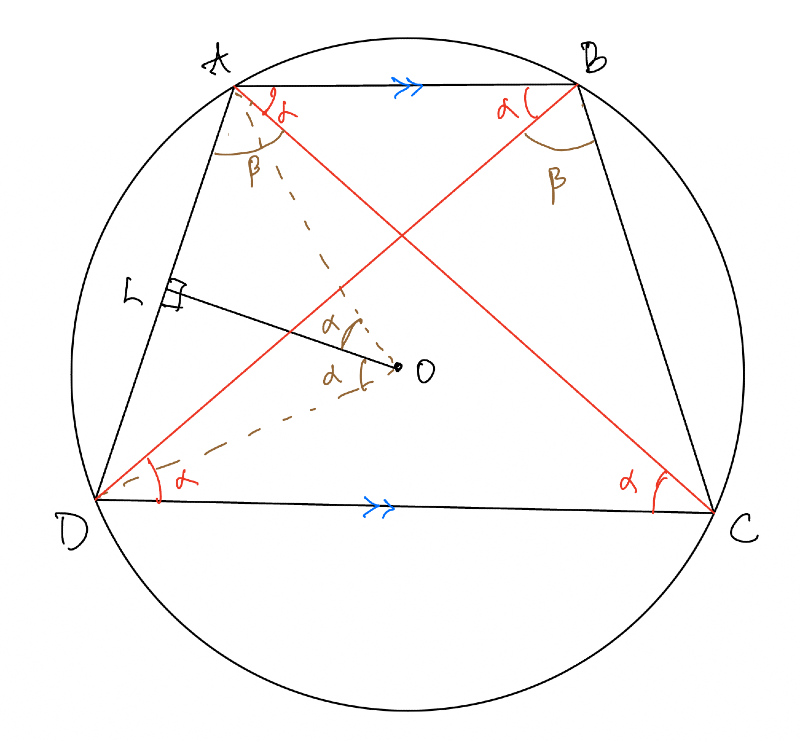
From triangle \( AOL \), we have:
$$
OL = R \cos \alpha
$$
From extended sine rule, we get:
$$
R(2R \sin (2\alpha + \beta) + 2R \sin \beta) = R \cos \alpha (2R \sin (\alpha + \beta) + 2R \sin (\alpha + \beta))
$$
Which reduces to:
$$
\sin (2\alpha + \beta) + \sin \beta = 2 \cos \alpha \sin (\alpha + \beta)
$$
This is a standard identity:
$$
\sin x + \sin y = 2 \sin \left(\frac{x + y}{2}\right) \cos \left(\frac{x – y}{2}\right)
$$
Comment: My student Rishon Fernandes pointed out this is a subproblem of BMO 2022 R1 P5.
RMO difficulty feeling: 3
The question counts chains in a divisor lattice. Let \( f(n) \) be number of chains. Known recursion:
$$
2f(n) = \sum_{d \mid n} f(d)
$$
This hints at Möbius inversion ideas. I like how this question has multiple approaches.
Proof: We write the divisors of \( 3 \cdot 2^m \) as a lattice diagram:
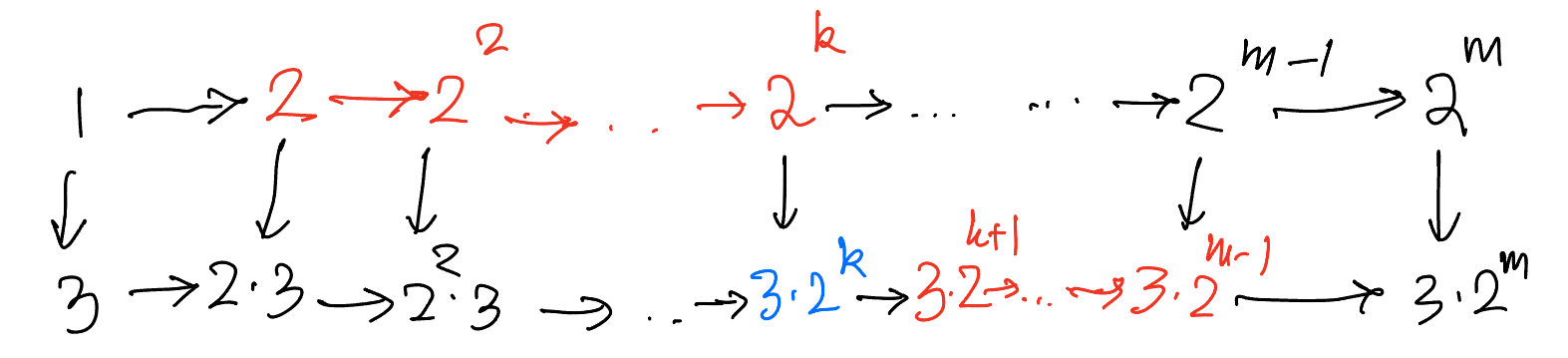
A maximal chain is one that can’t be enlarged. All go from 1 to \( 3 \cdot 2^m \). Let the switch from top row to bottom row happen at \( 3 \cdot 2^k \) for \( k = 0, 1, …, m \).
For \( k \ne m \): each maximal chain has \( m-1 \) red elements → \( 2^{m-1} \) subchains. With \( m \) such \( k \), we get \( m \cdot 2^{m-1} \).
For \( k = m \): we take subset of top row → \( 2^m \) chains.
Total:
$$
m \cdot 2^{m-1} + 2^m = (m+2) \cdot 2^{m-1}
$$
I liked solving this paper. Balanced RMO. I suspect the cutoff will be above 50 (due to 3 solvable problems) but below 70 (due to difficulty spike after that).
Update: Looks like I was right about the cutoff 👏
