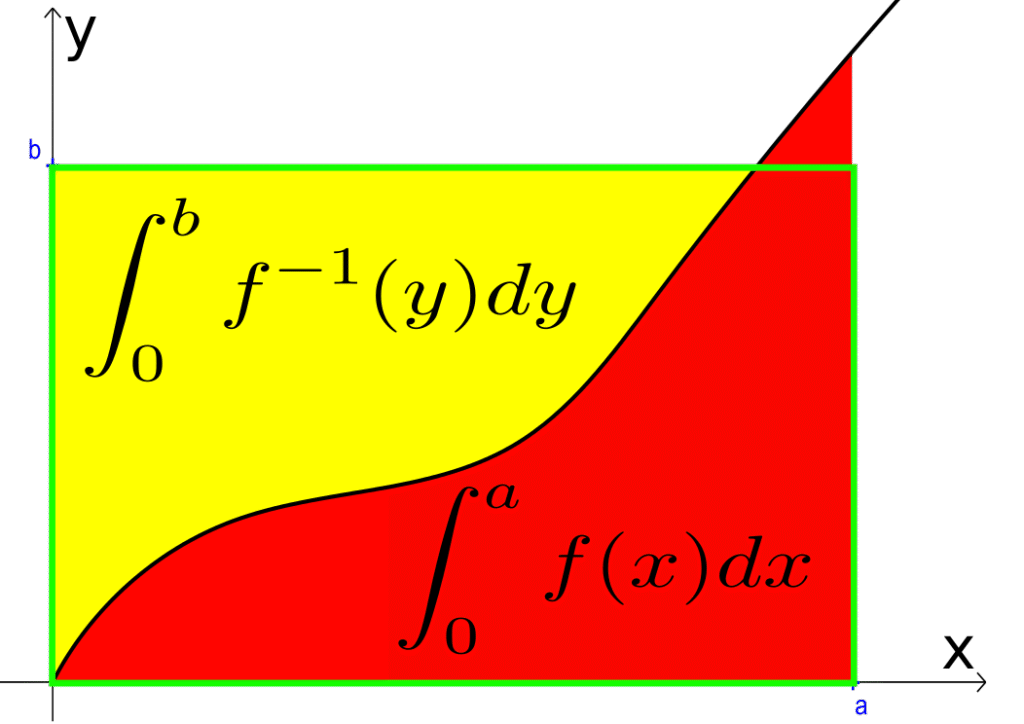
Combinatoral geometric inequality from IMO 1989
A beautiful application of double counting in combinatorial geometry The Problem Here’s a classic IMO 1989 problem that showcases the power of combinatorial reasoning in geometry: Problem: Let $n$ and $k$ be positive integers and let $S$ be a set of $n$ points in the plane such that: Prove that $k < \frac{1}{2} + \sqrt{2n}$. At […]